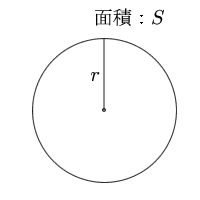
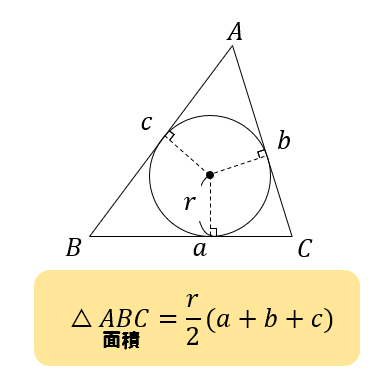
円の面積を求める公式は小学校で習いますが、なぜその公式になるのか? という 疑問 ( ぎもん ) は、高校2年生で 微分 ( びぶん ) を学習するまで分かりません! 他の面積公式との関係 この面積公式をもとに他の面積公式を導出することができます。 例えば,この公式と正弦定理を用いることで対称な式: S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます( R R R は三角形 A B C ABC A BC の外接円の半径)。 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2
円 面積の計算 計算サイト
円の面積 公式 直径
円の面積 公式 直径-円の面積の公式 円の面積は 『半径×半径×円周率』 で計算できます。 たとえば以下のような問題の場合。 例題 半径 2cm 2 c m の円の面積を求めよ。 答えはこのように求めることができます。 2 ×2× 314=1256(cm2) 2 × 2 × 314 = 1256 ( c m 2) つづいて、なぜ 円の面積=半径×半径×314 =7×7×314 =cm2 (2)円の面積=半径×半径×314の式から、面積÷314で、 (半径×半径)がわかる。




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さV = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
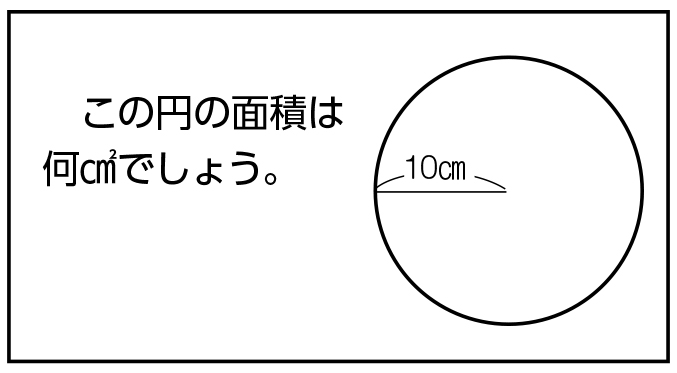
球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる円の面積 「半径×半径×円周率」で求められる円の面積。 いろいろな大きさの円の面積を計算してみよう。 動画で学ぼう! (NHK for School) 円の面積の求め方を、四角に直すことで原理から考える上の濃い肌色と薄い肌色の面積をあわせると、6985= 775 これを4倍すると元の円の面積になるので、775×4=310 約310 上のことから、 半径10cmの円の面積 は、 半径1辺とする正方形の面積 の 約31倍 であることをとらえさせます。
楕円の面積の公式は次のようになります。 楕円は「円を x 軸方向,または y 軸方向に拡大(縮小)したもの」 です。 これを利用すると,楕円の面積公式は簡単に導出することができます! 例えば,縦横 b の正方形を, x 軸方向に \displaystyle \frac {a} {b 円のまわりの長さを求めるときは 円周の長さ = 直径 × 円周率 三角錐の表面積 側面積 底面積 の求め方(公式) 写真の形の名前、側面積 底面積 表面積 の求め方を教えて下さいㅠㅠ 数学 半径×半径×πって、円の周の求め方ですか?



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
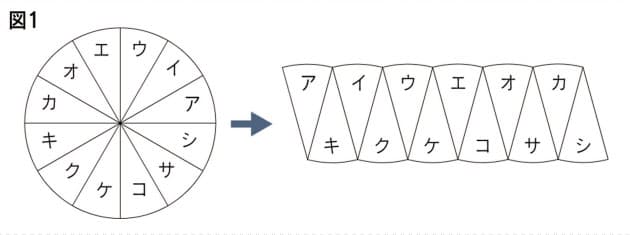
円の面積から半径を求める 円の面積から直径を求める 円の面積から円周を求める 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半円の面積の公式をつくってみよう。 《3/5の展開》 3 / 5 ・ 円を16等分したおうぎ形を並べ、その形から面積を推測する。 ・ 既習の図形と関連付けて、円の面積の公式を考える。 (作業的な活動) (説明する活動)



6年算数 円の面積 2 わかる教え方




円の面積 練習応用 Youtube
直径Dから面積Aに変換する計算は「A=πD 2 /4」です。 円周率と直径の二乗を掛けて4で割った値です。 また、直径Dと半径rは「r=D/2」の関係です。 よって半径から面積に変換する計算式は「A=πr 2 」です。円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h



円積率 雑学のソムリエ



円 の面積 計算ドリル 問題集 数学fun
さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr 2 となります。 円を直線で切った時の面積の計算方法を教えてください。 半径rの円の一番底からHの高さで直線で切った時の面積を計算する方法を教えてください。rとHだけの式でできるでしょうか? 図のように線を引き、 OABを定めるOA=rhとなるので、三平方の定理より、AB=√(2rhh^2)また、∠AOB=θとおくと



押川 隼也 高校 大学受験対策 中1数学 円周率p 円の面積 円周の長さ 1年生は事前に知っておいて損はなし 2年生は今のうちに軽く目を通して思い出しましょう 3年生は知っていたらrt 3年生は覚えてなかったらふぁぼって暗記



小6算数 円の面積 指導アイデア 1 みんなの教育技術
求積公式(平面) a=面積 正方形 長方形 平行四辺形 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正六角形 正八角形 正多角形 円 a=面積 円分 欠 円 環 形 扇 形円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 答え: 2 × 2 × 314 = 1256 (cm 2) 正確には 2 × 2 × π = 4 π
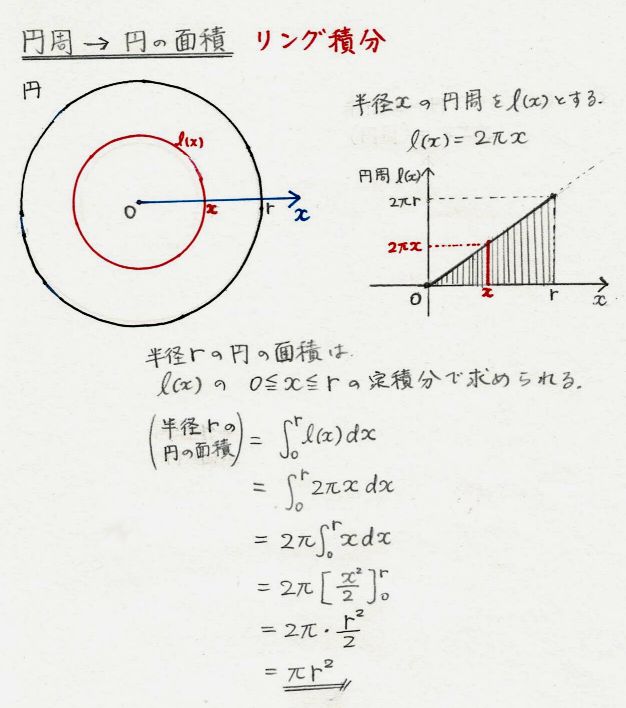



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



小6算数 円の面積 指導アイデア 2 みんなの教育技術
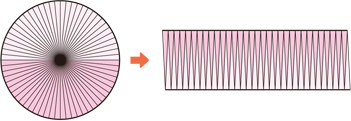
円がバームクーヘンやトイレットペーパーの ように層になってると考えます。 これを黒い縦の実線のところで、切って左右に広げます。 そうすると円は、円周を底辺、半径を高さ、とする三角形になり ます。 面積は 面積=円周×半径÷2 円周を 半径×球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314
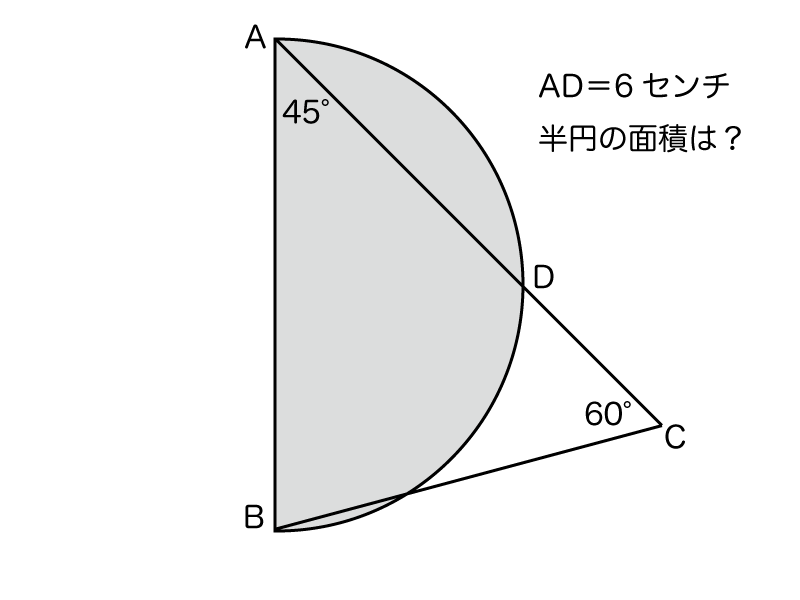



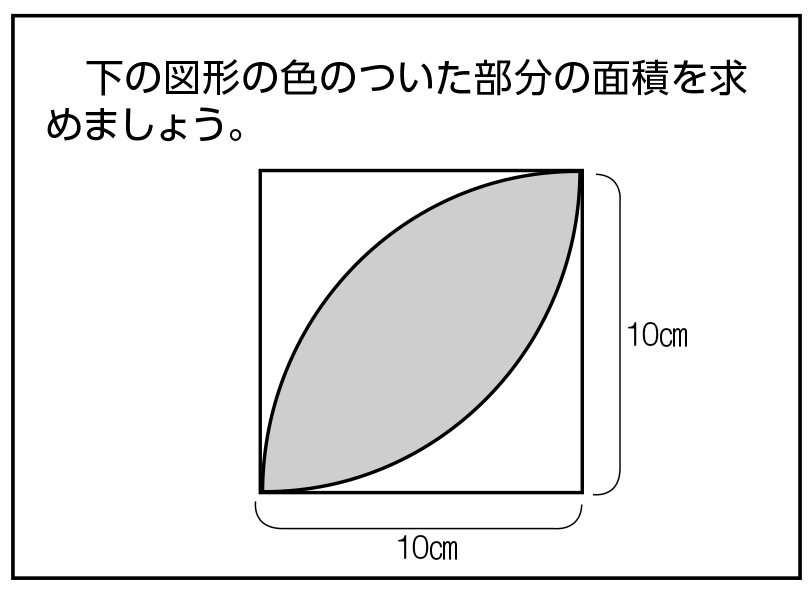
面積公式を組み合わせて解く半円の面積計算 受験算数入門




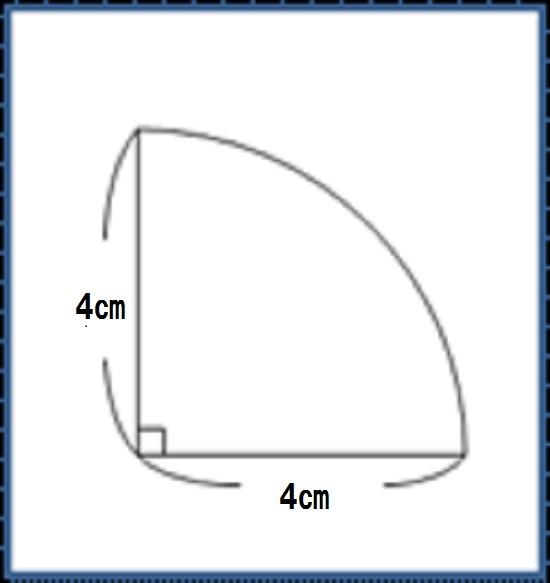
半円や4分の1の円 四分円 の面積を計算する方法 白丸くん
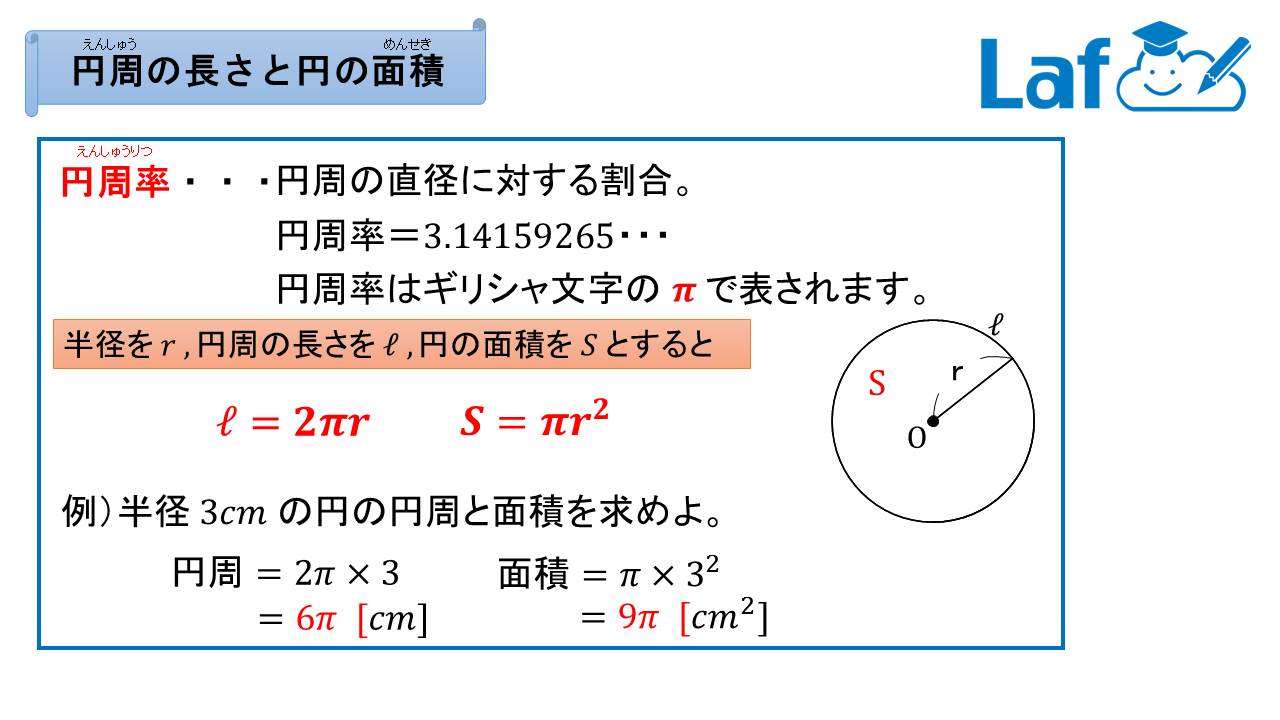
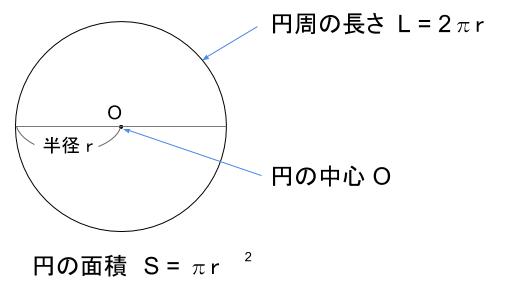
まず、円の面積と円周は以下の公式で求められます。 円の面積 S =πr2 S = π r 2 円周 l=2πr l = 2 π r(1)円や球の求積公式の導出法 ① 円の面積公式の導出法 半径r の円の面積S は,例えば,次のようにして求 めることができる。 関数 x のグラフと 軸で囲ま れる部分の面積は半円の面積を表すので, で 考え方は弧の長さと同様。 完全な円の面積( πr2 π r 2 )と比べて、扇形の割合をかけた値が扇形の面積になります。 『半径×半径×314× 中心角 360 × 314 × 中 心 角 360 』⇒『πr2 × a 360 π r 2 × a 360 』 5扇形の面積の公式(弧の長さからの導出)




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円の面積 小学生 算数のノート Clear
円の面積・・・半径×半径×π=πr² 円周・・・直径×π=2πr ここで登場するのが、『微分』です。 r²を微分すると2rになります。 つまり、円の面積を微分すると円周の公式になります。 球の体積・・・4πr³/3 球の表面積・・・4πr² 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p




小6 算数 小6 2 円の面積 応用編 Youtube



動画で学習 1 円の面積 算数



1




円の面積 算数用語集



子供に説明できる 円の面積の公式 の証明 Nikkei Style




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



半径10cmの円の面積を求める公式は10 10 3 14 314m2で Yahoo 知恵袋




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
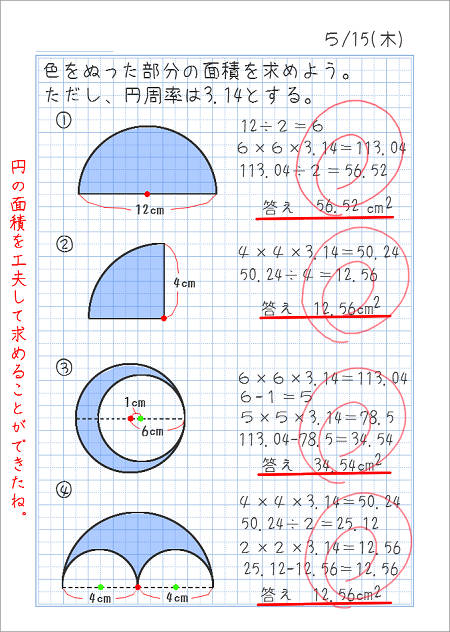



円の面積 その1 家庭学習レシピ
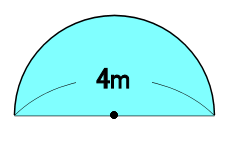



円の面積 半径




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
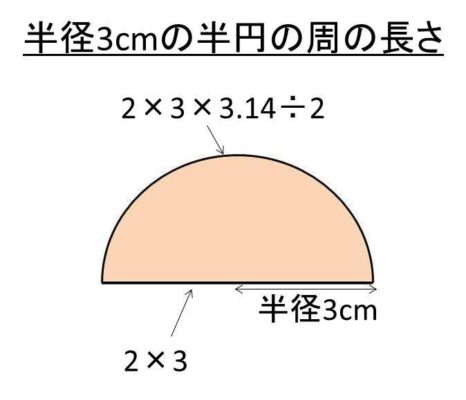



半円の周の長さの計算方法 白丸くん



6年算数 円の面積 2 わかる教え方



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su



円の面積と公式 面積計算機




円の面積応用b 小学校 算数 学習ノート 中学 勉強
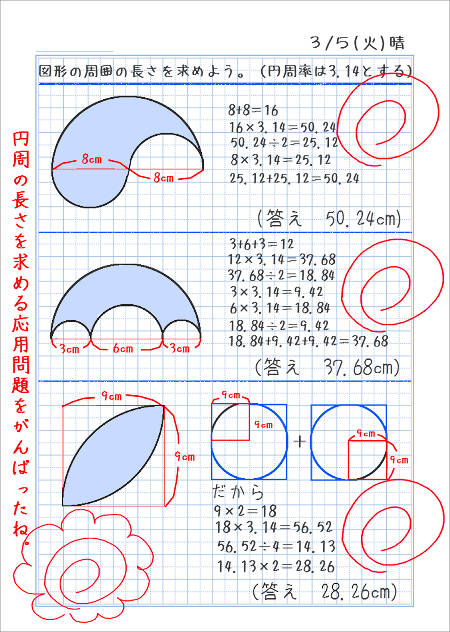



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
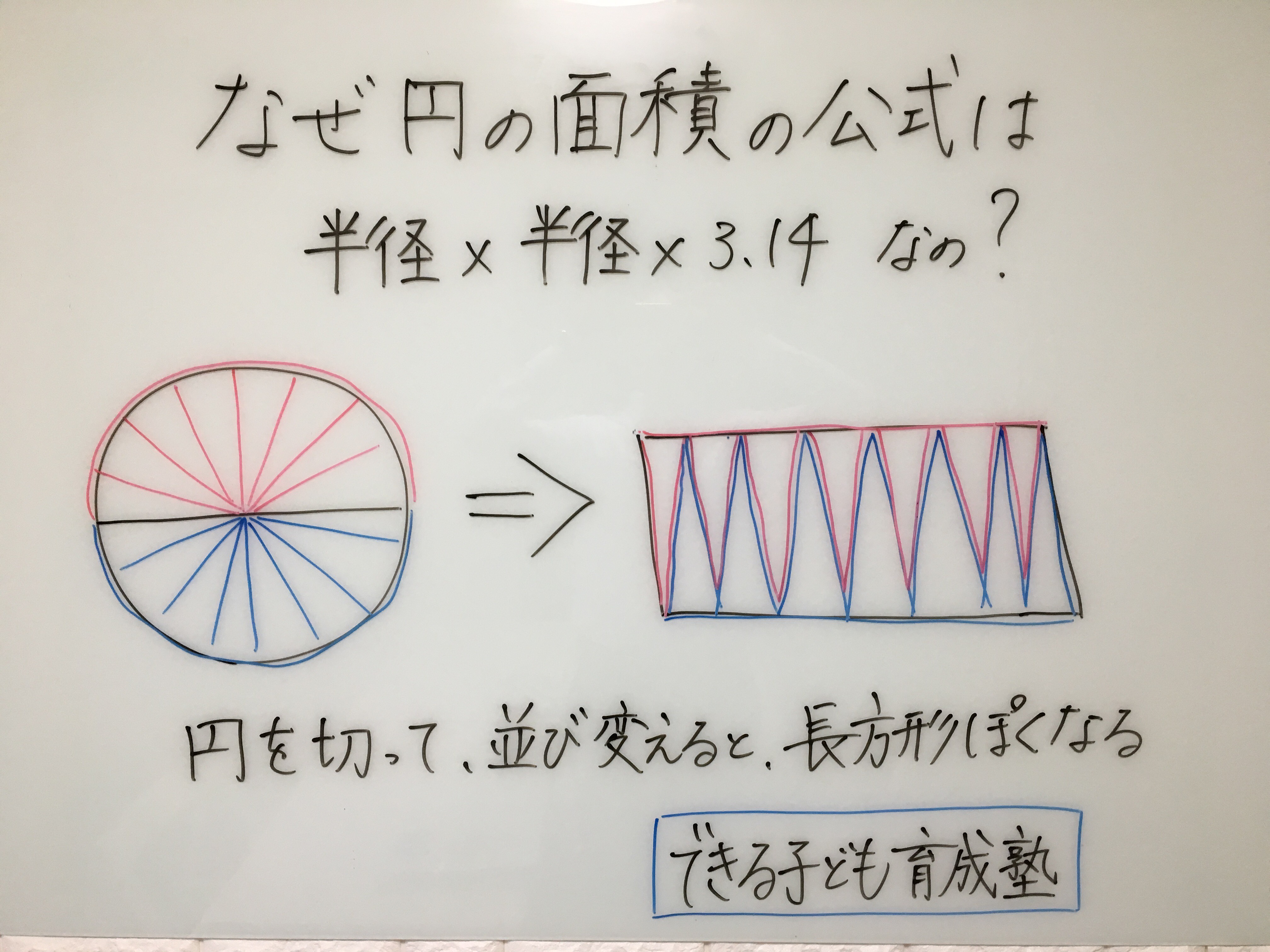



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の 小学生専門 国語と算数の苦手を克服
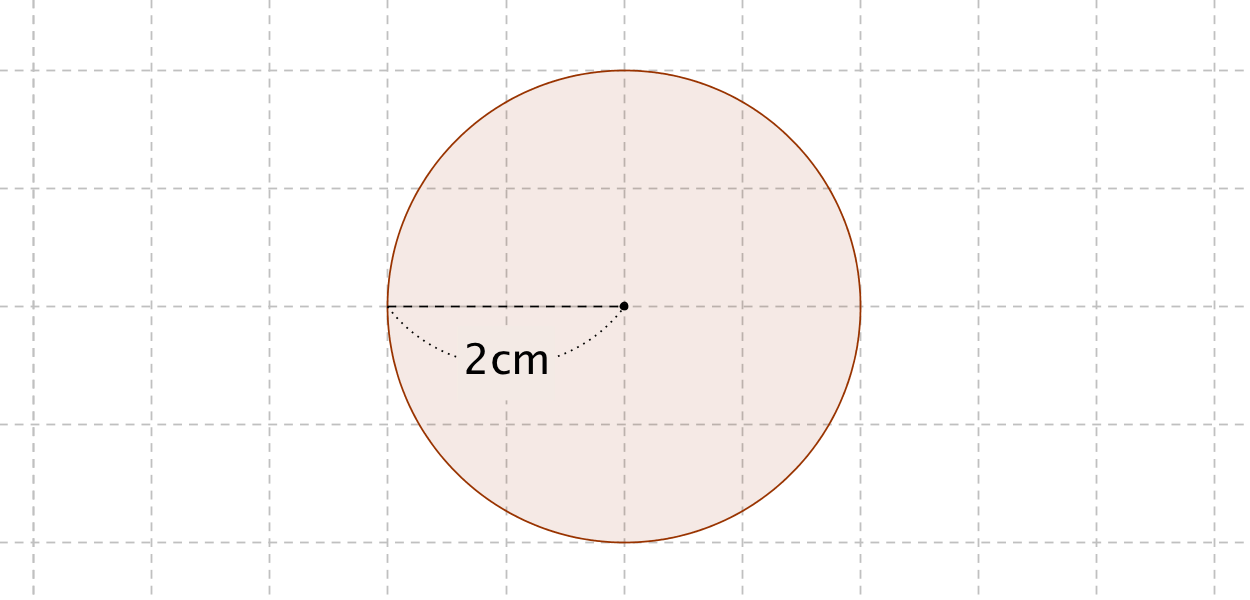



円の面積の公式 算数の公式




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
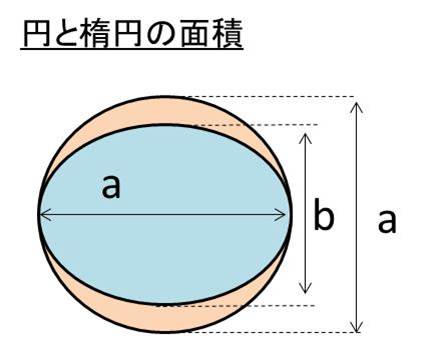



X Acos8とy Bsin8の面積の計算方法は 楕円の面積の一部の求め方は 楕円の面積と円の面積 ウルトラフリーダム



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora




弓形の面積 香料ゐっすゐの夢
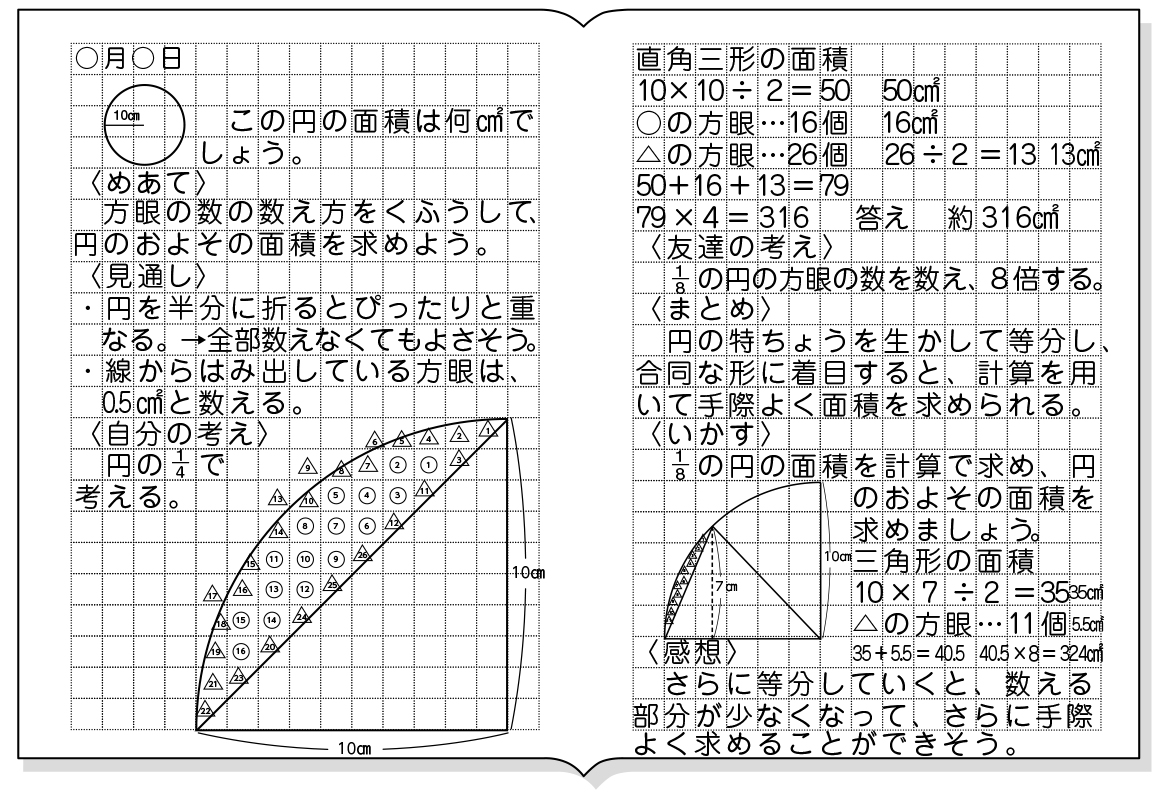



小6算数 円の面積 指導アイデア 1 みんなの教育技術



6年算数 円の面積 2 わかる教え方




6年算数 円の面積 1 アニメでわかる教え方




円周や円の面積を求めるときに使う円周率3 14ってなに みけねこ小学校




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




6年 円の面積まとめプリント ネコ好きな学校の先生の日常




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




扇形の面積の求め方 公式と計算例
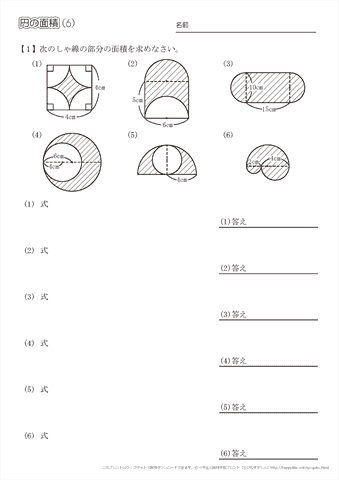



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
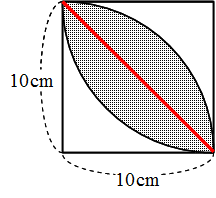



世界一やさしい 円の面積を求める問題の解き方 働きアリ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




小6 算数 小6 旧 円の面積 Youtube




円の面積 半径 半径 円周率なのはなぜ 永和進学ゼミ 個別指導ソフィア 学習塾ブログ




円の面積 算数用語集




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




円 面積の計算 計算サイト




円 扇形 の面積 周や弧の長さの公式 数学fun



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋
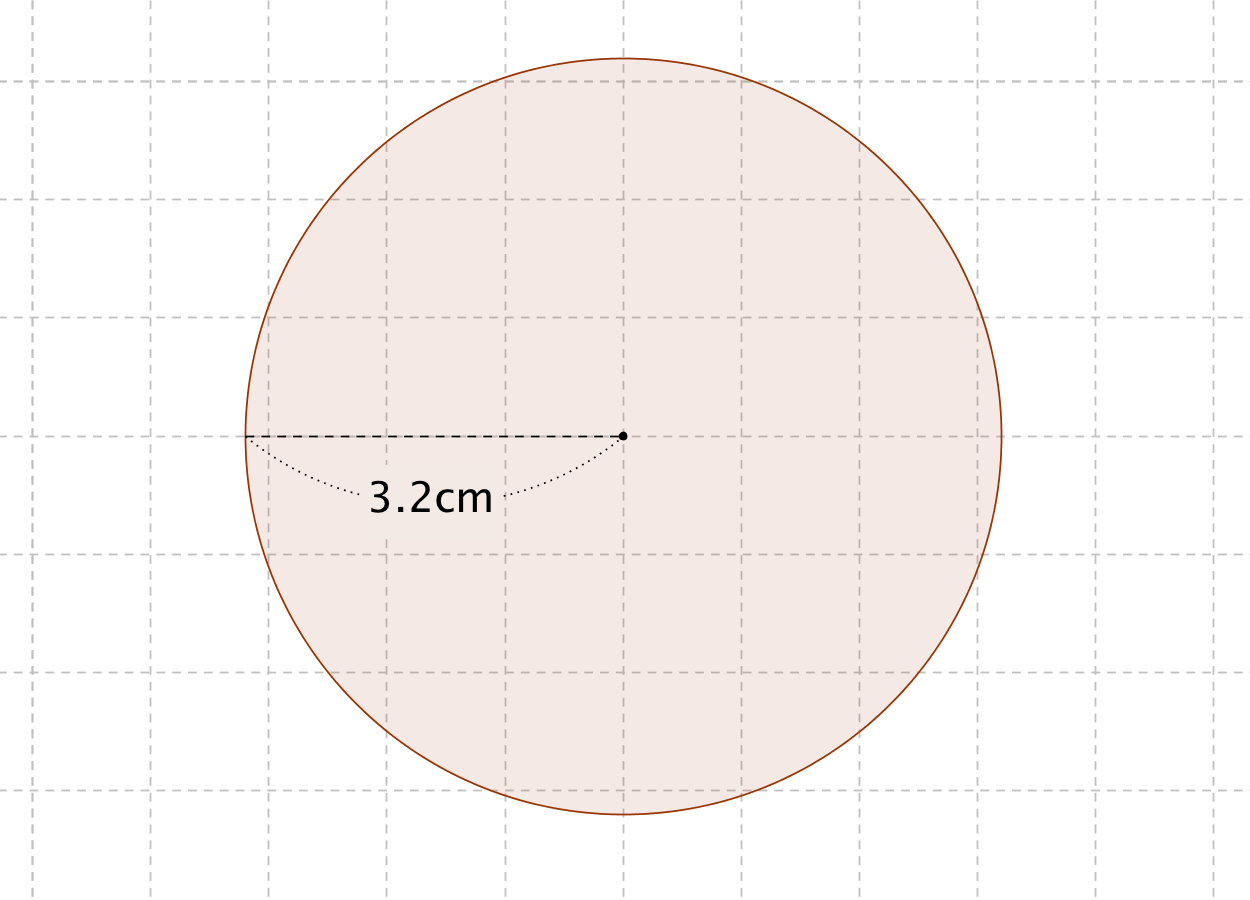



円の面積の公式 算数の公式




円の面積の求め方 公式と計算例




円の面積3 小学校6年生の教科書から つづき 身勝手な主張



円の面積 算数用語集




小6 円 円の面積の求め方 日本語版 Youtube




円の面積 円周の求め方 公式 小学生 中学生の勉強



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora




円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 中学数学
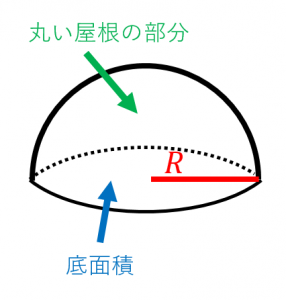



半球の体積と表面積を計算する 具体例で学ぶ数学




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
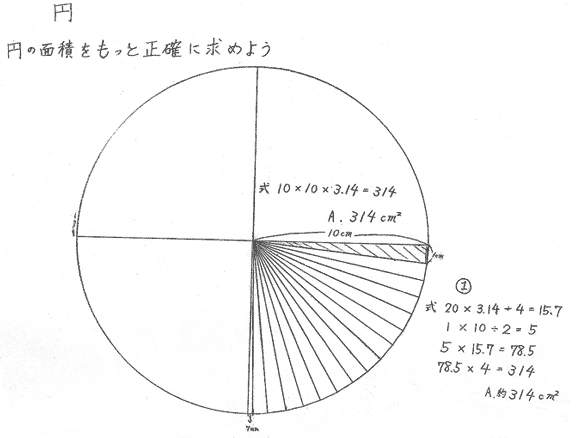



実践記録算数5年




円の面積の求め方 公式と計算例



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb




円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト
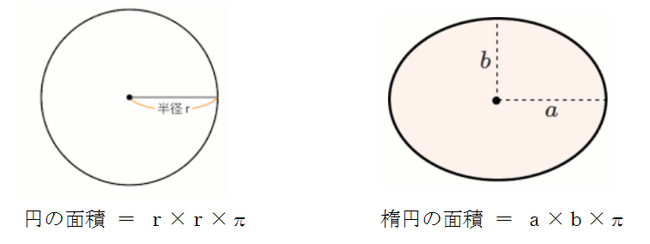



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師



円の面積の公式 この問題をやれば円の面積は余裕だぜ 三重の個人契約家庭教師



円の面積 円周の求め方 公式 小学生 中学生の勉強



3



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
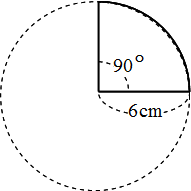



世界一やさしい 円の面積を求める問題の解き方 働きアリ




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun
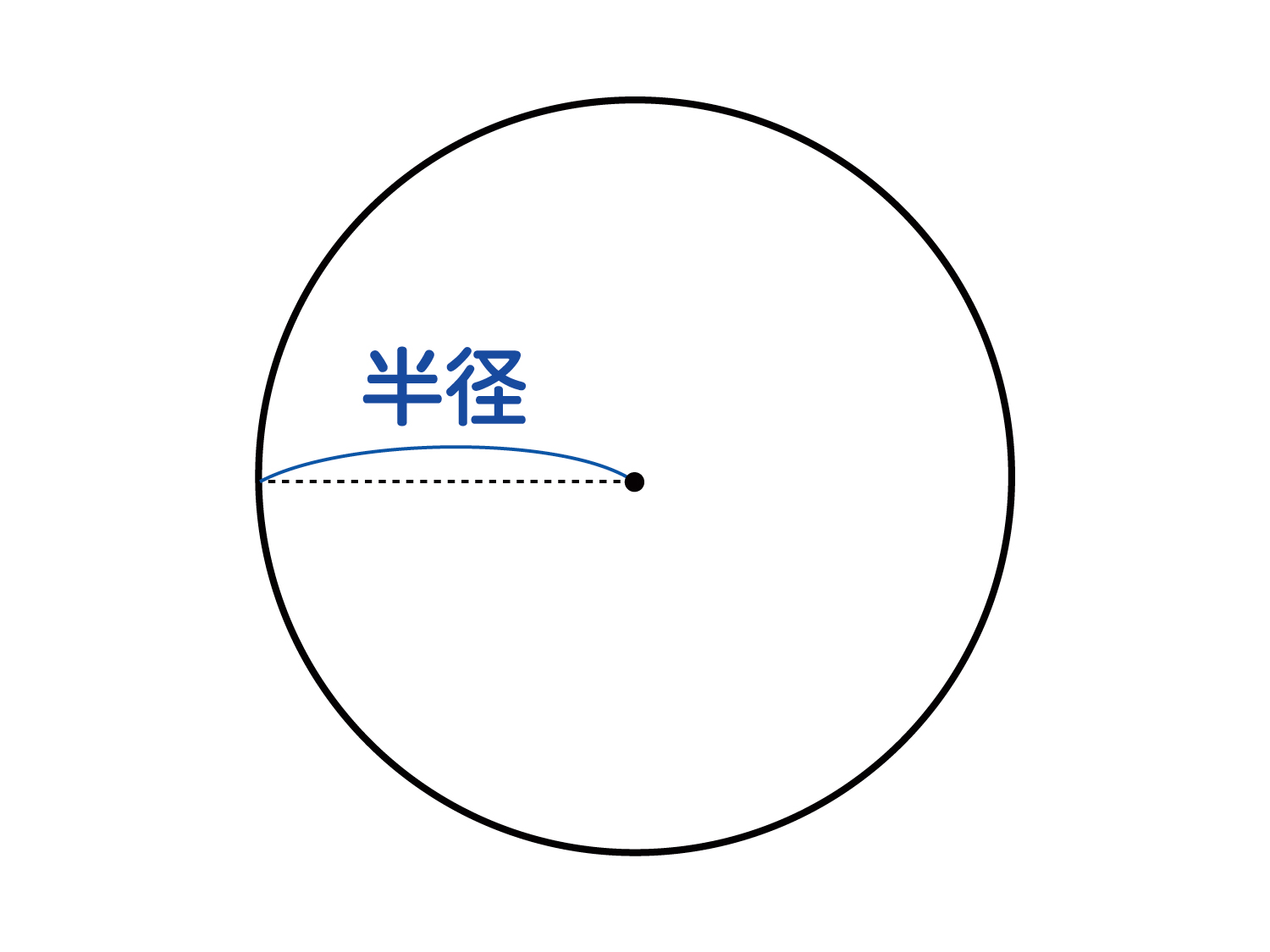



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円周の求め方と円の面積について アタリマエ
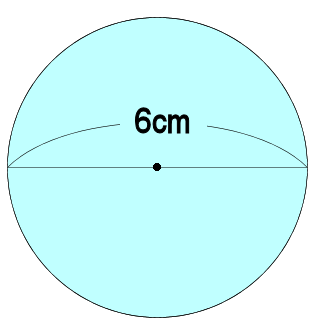



円の面積 直径
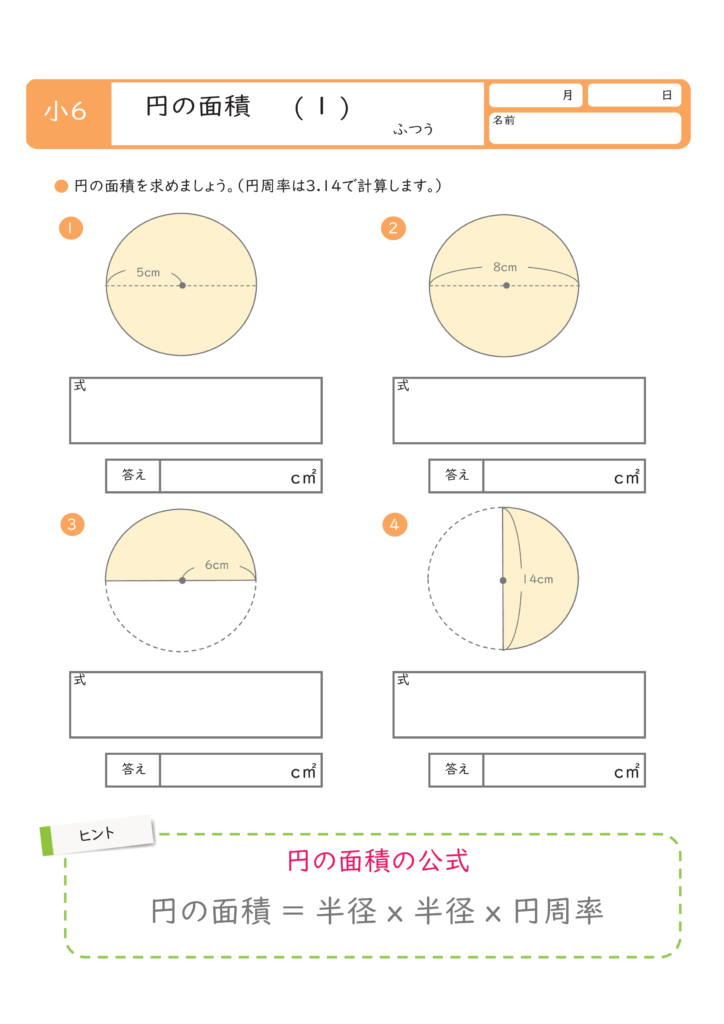



こどもプリント 円の面積 無料プリント




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
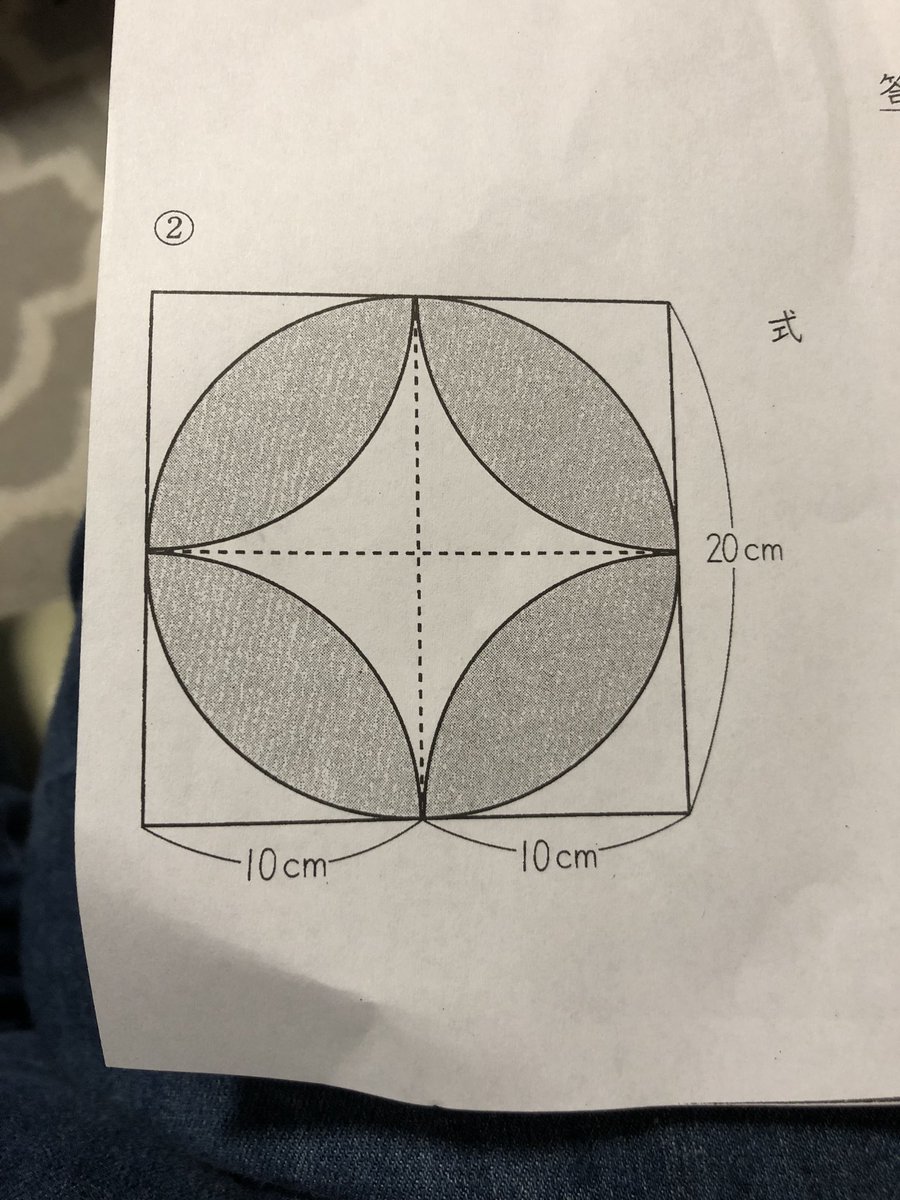



円の面積
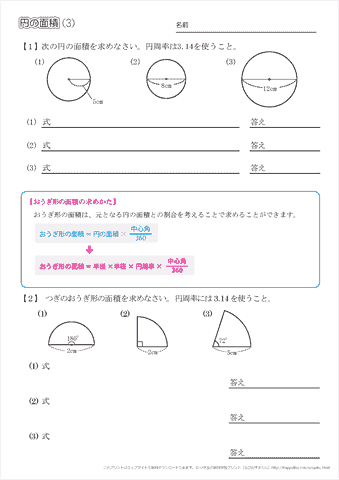



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
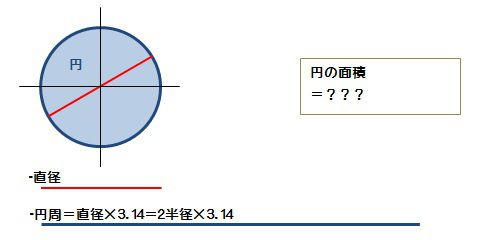



円の面積 算数の公式覚えてますか



1
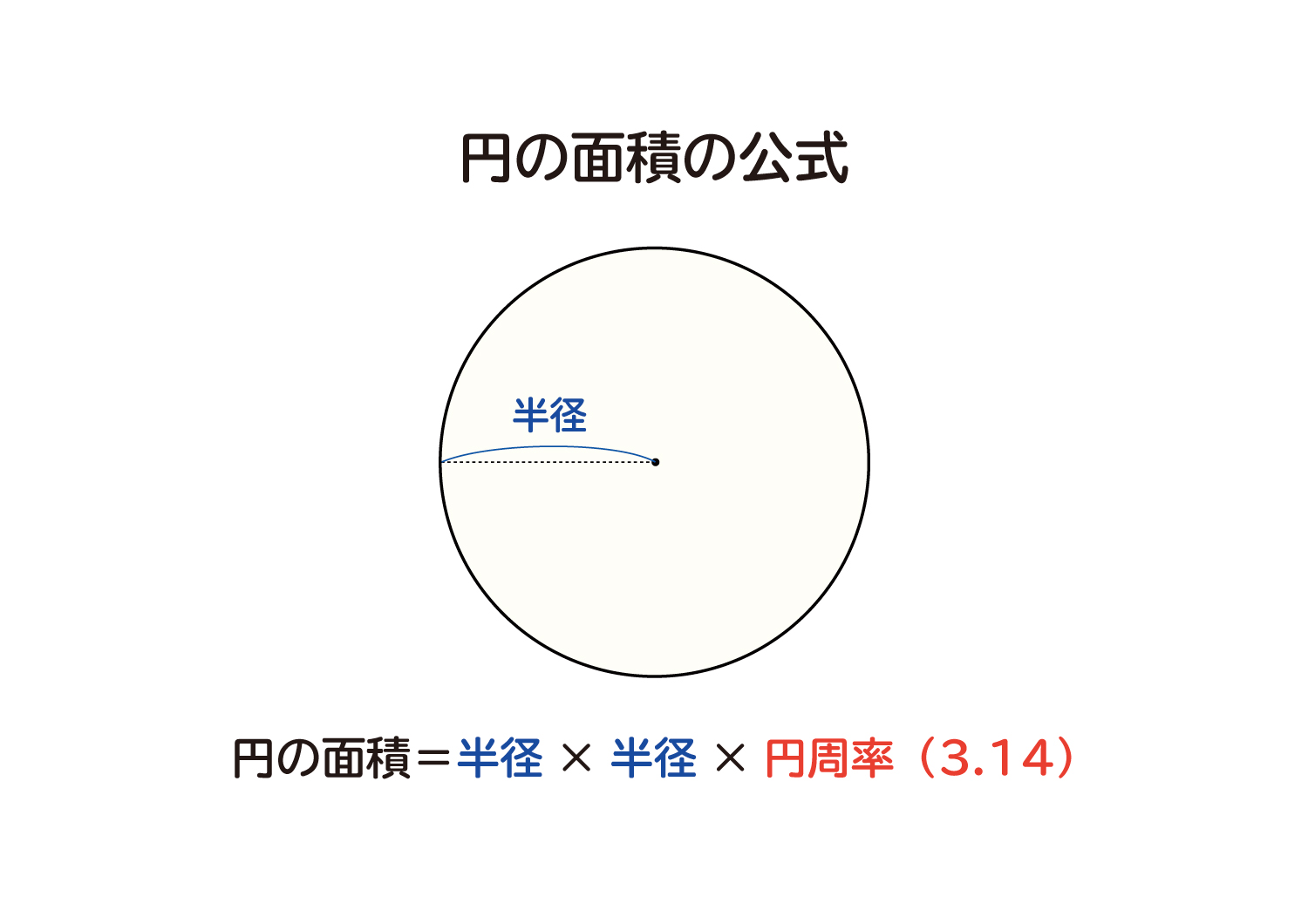



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張




円の面積の公式 算数の公式
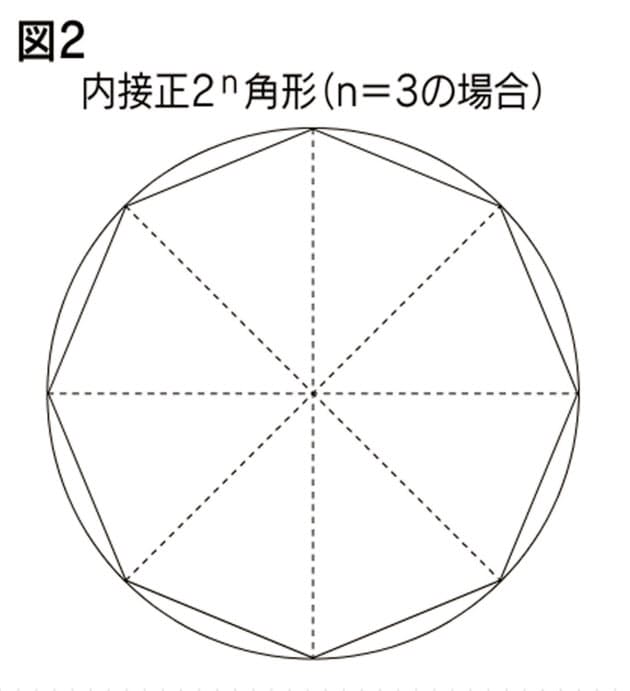



子供に説明できる 円の面積の公式 の証明 Nikkei Style




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積の求め方 公式と計算例




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト
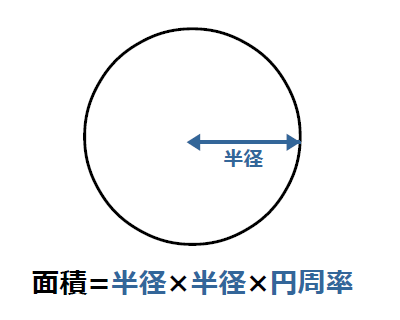



円の面積計算 ゆるゆるプログラミング



気まぐれ Net 図を用いた円の面積の求め方 公式を使わずに




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント
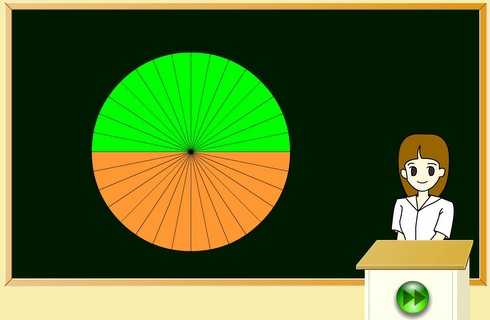



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ



0 件のコメント:
コメントを投稿